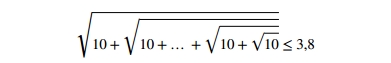| [10 Дек 2022] | |
| Свежая информация (0) | |
| [14 Окт 2016] | |
| Hазбор входного тестирования «Кенгуру»! (0) | |
| [09 Июл 2016] | |
| Mathematics without borders (0) | |
| [26 Апр 2016] | |
| Всероссийская смена «Юный математик» в ДЦ «Орленок» (0) | |
| [25 Апр 2016] | |
| Домино (0) | |
| [22 Апр 2016] | |
| Летняя школа «Фоксфорда» (0) | |
- 2006 Декабрь
- 2007 Январь
- 2007 Ноябрь
- 2008 Январь
- 2008 Февраль
- 2008 Апрель
- 2008 Октябрь
- 2008 Ноябрь
- 2008 Декабрь
- 2009 Январь
- 2009 Февраль
- 2009 Март
- 2009 Апрель
- 2009 Май
- 2009 Сентябрь
- 2009 Октябрь
- 2009 Ноябрь
- 2009 Декабрь
- 2010 Январь
- 2010 Февраль
- 2010 Март
- 2010 Апрель
- 2010 Май
- 2010 Июнь
- 2010 Июль
- 2010 Август
- 2010 Сентябрь
- 2010 Октябрь
- 2010 Ноябрь
- 2010 Декабрь
- 2011 Январь
- 2011 Февраль
- 2011 Март
- 2011 Апрель
- 2011 Май
- 2011 Август
- 2011 Сентябрь
- 2011 Октябрь
- 2011 Ноябрь
- 2011 Декабрь
- 2012 Январь
- 2012 Февраль
- 2012 Март
- 2012 Апрель
- 2012 Май
- 2012 Июнь
- 2012 Июль
- 2012 Август
- 2012 Сентябрь
- 2012 Октябрь
- 2012 Ноябрь
- 2012 Декабрь
- 2013 Январь
- 2013 Февраль
- 2013 Март
- 2013 Апрель
- 2013 Август
- 2013 Сентябрь
- 2013 Октябрь
- 2013 Ноябрь
- 2013 Декабрь
- 2014 Январь
- 2014 Февраль
- 2014 Март
- 2014 Апрель
- 2014 Май
- 2014 Сентябрь
- 2014 Октябрь
- 2014 Ноябрь
- 2014 Декабрь
- 2015 Январь
- 2015 Февраль
- 2015 Апрель
- 2015 Декабрь
- 2016 Январь
- 2016 Февраль
- 2016 Март
- 2016 Апрель
- 2016 Июль
- 2016 Октябрь
- 2022 Декабрь
07:28:12 Заочный конкурс по математике | |
Заочный конкурс по математикеВесенний тур 2013 годаДорогой друг! Приглашаем тебя принять участие в заочном конкурсе по математике и информатике. Участвовать в нём может любой ученик 6-8 класса, решивший по крайней мере пять из предлагаемых 20 задач. Для этого он должен не позднее 20 марта выслать полные решения задач обычным письмом (не заказным) по адресу Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс.
На письме должен быть указан обратный адрес, включая имя и фамилию. В письмо следует вложить два пустых незаклеенных конверта с маркой, написав на них свой адрес (В одном конверте будут посланы результаты проверки и приглашение на разбор. Другой конверт может быть использован для информации о заочном конкурсе, математических кружках, олимпиадах и пр.) На каждом листе работы просим указывать фамилию, имя, номер школы и класс. В письмо следует вложить заполненную карточку участника (см. на обороте). Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), а также по электронной почте: zmk@mccme.ru. (Очень просим Вас НЕ присылать решения по электронной почте.) Информация о заочном конкурсе имеется в Internet на сайте http://www.mccme.ru/zmk/. В частности, на этом сайте будет указана дата разбора задач (скорее всего, это будет в мае), а после разбора помещён список победителей конкурса. На сайте http://www.mccme.ru/ имеется также информация о математических кружках, олимпиадах и пр. Информацию о кружках можно получить также по телефону (499)~241-05-00. Желаем успеха! 1. Разрежьте квадрат на три части и сложите из них неравнобедренный непрямоугольный треугольник (то есть треугольник, у которого все стороны разные и все углы отличны от 90°). 2. Укажите наименьшее целое положительное число, которое не является делителем числа 31! = 1·2·3·…·30·31. 3. Можно ли разбить число 174 на три различных целых положительных слагаемых так, чтобы сумма любых двух из них делилась нацело на третье? 4. Составьте три несократимые дроби, дающие в произведении единицу, используя в качестве числителей и знаменателей целые числа от 1 до 9 (каждое число можно использовать не более одного раза). 5. Все натуральные числа от 1 до 2013 разбиты на две группы: чётные и нечётные. В какой из групп сумма всех цифр, использованных для записи чисел, больше и на сколько? 6. Из городов А и Б одновременно направились навстречу друг другу два пешехода. После встречи первому осталось идти (до города, куда он направляется) ещё a часов, второму — b часов. Сколько часов прошло от начала движения до встречи? (Пешеходы двигались с постоянными скоростями.) 7. Можно ли так упаковать в ящик 2×2×2 три цилиндра высотой 2 и диаметром 1, чтобы ни один из них нельзя было сдвинуть с места, не смещая других? 8. Найдите последнюю цифру произведения всех нечётных трёхзначных чисел. 9. Сто разных фишек положены в ряд. Любые две фишки, стоящие через одну, можно поменять местами. Можно ли с помощью нескольких таких операций переставить фишки в обратном порядке? 10. В круге проведено m хорд, которые пересекаются внутри круга в n точках (в каждой точке по 2 хорды). На сколько частей они делят круг? 11. Можно ли какой-то прямоугольник разрезать на три прямоугольника, подобных исходному, причём так, чтобы все три имели разные размеры? (Прямоугольники называются подобными, если у них одинаковая форма, то есть одинаковое отношение большей стороны к меньшей.) 12. Из одной заготовки можно сделать одну деталь, а из стружек от 6 заготовок можно изготовить целую заготовку. Сколько деталей можно получить из 600 заготовок? 13. Сколько существует различных шестигранных игральных костей с цифрами 1,…,6 на гранях? (Две кости считаются одинаковыми, если их можно повернуть так, чтобы числа на соответствующих гранях совпали.) 14. Дано десять чисел; сумма любых трёх из них чётна. Докажите, что все числа чётны. 15. В неизвестном месте поля 10 на 10 для игры в морской бой расположен «линкор» — прямоугольник размером 4 на 1. Какое минимальное число выстрелов нужно сделать, чтобы гарантировать, что будет попадание? Куда нужно стрелять? Можно ли обойтись меньшим числом выстрелов? 16. Работа была поделена поровну между работниками в бригаде. После первого дня посчитали, сколько человек выполнило не менее 30% своей доли — таких оказалось 70% всех работающих. Когда стали считать только тех, кто выполнил не менее 70% своей доли, таких оказалось 30% работавших. Можно ли быть уверенным, что выполнена хотя бы треть работы? 17. Докажите, что
(при любом количестве квадратных корней в левой части). 18. Какая средняя сумма цифр у четырёхзначного числа? (Четырёхзначные числа — от 1000 до 9999; у каждого из них вычислили сумму цифр, а потом взяли их среднее арифметическое. Напомним, что среднее арифметическое k чисел a1,…,ak определяется как их сумма, делённая на их количество, то есть как (a1+…+ak)/k.) 19. Можно ли так нарисовать внутри квадрата несколько непересекающихся круглых клякс, чтобы общая площадь, покрытая кляксами, была больше 99% от площади этого квадрата? 20. Докажите, что в любой бесконечной последовательности целых положительных чисел a1,a2,… найдётся пара чисел ai и aj, в которой i<j и число ai можно получить из aj вычёркиванием некоторого числа цифр в десятичной записи (возможно, ни одной: ai=aj тоже допускается). | |
|
| |
| Всего комментариев: 0 | |